글
정리 중인 자료입니다.
참고자료
[제4판] 현대통계학 (박정식, 윤영선) 13장. (p.293-)
에듀팜 [SPSS기초] 17장-27장
t-검정은 언제 사용하는가?
모집단의 평균을 알고 있고,
표본의 평균과 분산을 알고 있을 때
표본의 평균이 표본의 평균과 같은가 다른 가를 검정하는 것.
예를 들어보자.
예제1.
일본 초등학생들의 IQ 평균이 105라고 하자. 한국의 100명의 초등학생들을 표본으로 IQ를 검사해보니 평균이 110이 나왔다. 그러면 한국의 초등학생들이 일본 초등학생보다 IQ가 높다고 결론 내릴 수 있는가? (이 결론을 내리기 위해서는 사실 100명의 표본 초등학생에 대한 분산 정보가 필요하다.)
예제2.
2000년대 한국 고3학생들의 키가 165cm 였다고 하자. 최근(2009년) 고3학생 200명을 표본으로 키를 측정해보니 평균이 170cm 가 나왔다. 그러면 학생들의 키가 이전보다 증가되었다고 결론을 내릴 수 있는가?
t-검정 검정 방법
간단하게 t-검정을 하는 방법을 설명한다.
표본에 대하여 t-검정 통계량 값을 계산한다. (-4에서 4정도 사이의 값을 얻게 된다.)
그 값이 t-분포의 그래프의 양 끝 쪽에 속할 수록 모집단과 평균이 다르다는 것을 보여준다.
지정한 유의확률(%)을 가지고 유의값을 선정하여 검정할 수 있다.
좀 더 자세하게 t-검정을 분류해 볼 수 있다.
* 1표본 t-검정 (또는 일표본 t-검정)
* 독립 2표본 t-검정
* 대응 2표본 t-검정
위의 예제1, 예제2는 모두 1표본 t-검정에 속하는 예이다.
독립 2표본 t-검정이란?
위에서 t-검정은 모집단의 분포를 모르고, 표본 집단에서의 분포(평균, 분산)을 아는 상황인 것을 기억하자.
독립 2표본 t-검정이란 2개의 표본을 추출한 후 이 두개 집단의 분포(평균, 분산) 정보를 이용하여 두 표본의 모집단에 차이가 있는지를 검정하는 것이다.
예를 들어, 한국 고3학생 100명의 키를 측정하고, 일본 고3학생 100명의 키를 측정한 후 이 표본 데이터를 기초로하여, 한국, 일본 고3학생의 키에 차이가 있는가에 대한 결론을 얻고 싶을 때 독립 2표본 t-검정을 수행한다.
대응 2표본 t-검정
한 개체에게서 2회의 반응값을 얻은 경우 그 차이가 존재하는 가를 검정한다. 즉, 한 개체에 대하여
이름에서 [대응]은 짝(Pair)를 의미한다.
다시 말하면, 두번의 반복측정에서 얻어진 결과가 차이가 있는 지를 비교한다.
두 모집단의 원자료를 각각 요약하는 것이 아니라 대신 차이값의 자료를 얻고자 한다.
예를들어, 새로 개발된 간수치안정제가 효과가 있는지를 검정한다고 해보자. 10명의 환자에 대하여 개발된 약을 먹기 전과 후의 간 수치를 측정한다. 이 실험 값을 토대로 하여 간의 수치를 개선하는 효과가 있는 지를 검정한다. (이 실험에서 한 사람에 대하여 2개의 값이 쌍으로의 성격을 갖는다.)
비슷한 예로, 감기약을 먹기 전과 후의 몸의 열의 변화가 생기는지를 검정한다고 하자. 10명의 환자에 대하여 먹기 전과 먹은 후의 값(쌍, 대응)들을 얻는다.
다른 예로, A사건이 발생하기 이전과 이후의 특정 당(한나라당)에 대한 지지율의 변화가 발생했는 지를 검정한다고 해보자. 100명의 사람을 대상으로 하여 A사건 이전의 한나라당에 대한 지지율과 A사건 발생 후의 한나라당에 대한 지지율을 측정한다.
다른 예로, 어떤 교육단체에서 독서를 통한 심리안정 치료 방법을 개발했다고 하자. 100명의 정서장애자들에게 대하여 교육을 받기 전과 받은 후의 정서장애 정도를 측정한다.
-----------------------------
그럼, t-검정과 Z-검정의 차이를 살펴보자.
Z검정은 모집단의 평균과 분산을 모두 알고 있을 때, 어떤 레코드 또는 표본 집단이 모집단에 속하는가를 검정하는 것이다. 즉, t-검정은 모집단의 평균을 알지만 분산은 모른다는 점에서 차이가 있다.
모집단의 분산을 모르기 때문에 레코드들이 Z-분포를 한다고 말할 수 없다.
따라서 그러한 경우 t-분포를 따른다고 할 수 있다. (t-분포는 정규분포와 유사한 모양을 갖지만, 더 넓게 펼쳐진다는 차이가 있으며, 그 정도는 표본집단의 분산과 레코드의 개수를 가지고 결정된다.)
Z-분포와 t-분포의 차이를 살펴보자.
Z-분포는 모집단의 평균과 분산을 알고 있을 때의 정규분포를 의미한다.
반면, t-분포는 표본집단의 평균과 분산, 그리고 자료(레코드) 수를 알고 있을 때의 분포를 의미한다.
Z-분포 ----> 정규분포를 따른다.
t-분포 ----> 자유도가 (n-1)인 t-분포를 따른다.
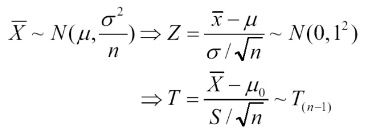
'스터디 자료' 카테고리의 다른 글
| 영어로 발표하는 방법 (0) | 2009.10.16 |
|---|---|
| [통계학] F-검정 (0) | 2009.10.14 |
| [통계학] 표준정규분포표 (Standard Normal Distribution Table) (0) | 2009.10.11 |
| [참고] 베이지안 네트워크 원리 (참고자료) (1) | 2009.10.10 |
| [통계학] 카이제곱분포표 참고 (엑셀 함수 이용 방법 추가 : ChiInv ChiDist) (0) | 2009.10.09 |

RECENT COMMENT